Look at a slime mold - the last thing anyone would think of is a living thing capable of figuring things out for itself. However, this is not the case at all. Slime molds, particularly true slime molds, which consist of a certain form of an amoeba, need to be able to move around their microenvironment, even if to find food, avoid harmful stimuli and respond to other pertinent factors in their lives. This is particularly hard when they also need to co-ordinate an amorphous slimy body in order to do so.
However, these slime molds exhibit the ability to conform to certain natural and physical laws. The ability to do so, even if they have no real ‘brain’ to help out, is an evolutionary advantage that enables life-forms such as these molds to feed efficiently, keep away from anything harmful and find an acceptable place (most often the bark of a tree or among fallen leaves) to live. In fact, the ability to move with this kind of purpose and efficacy is a common defining feature of living creatures, maybe the essential building blocks of consciousness, and are the point at which physics meets biology.
Physics at a Biological Level
This capacity, therefore, is of interest to scientists in the physical disciplines. It enables them to study these properties in systems that do them virtually on ‘automatic’ without the need to employ the extensive (and possibly expensive) computing hardware needed to study these bio-physical topics in detail. As a result, researchers have found that organisms such as amoebae are capable of solving problems that can be complex, although simple in theory, and time-consuming to actually work out, even when done on a computer.
Take the Travelling Salesman Problem (TSP). This is a task in which the solver is presented with the idea of a number of locations (most often known as ‘cities’ for the purposes of the TSP) and is required to find the shortest and best route between them. The ‘salesman’ needs to start at one ‘city,’ visit every other one only once, then travel back to the initial city.
Seems simple, right? Not really.
With increasing city numbers, the number (n) of possible solutions increases exponentially ((n − 1)!/2, in fact). Therefore, while the solutions when n is four equals three, this number grows to 2,520, when n is simply doubled. Therefore, the TSP is categorized as a non-deterministic polynomial time-hard (or NP-hard) problem. It can also be complicated further by applying varying distances to some of the inter-city routes. These days, TSPs with high n-values are best solved using either classic CPU-based processing or machine learning.
Amoeba and the Travelling Salesman
Now, throw TSP at a slime mold, and something interesting happens.
It seems that this organism is also quite adept at finding the best and most efficient routes from ‘city’ to ‘city.’ Obviously, this conclusion cannot be arrived at by asking the amoeba directly! Construct a microenvironment that simulates the problem, and it seems that the life-form can work it out pretty well.
The amoeba in question here is Physarum polycephalum or the ‘many-headed’ true slime mold. It is also known as a plasmodium, in which a single ‘unit’ of this mold exists as a basic lump of protoplasm, an amorphous tissue with some central veins for nutrient distribution. The amoeba can extend itself outwards from this lump in the form of ‘streamers’ or long, thin pseudopodia, in search of food or perhaps better-living conditions. The plasmodium also does this to achieve equilibrium or the evenest distribution of its own mass across a surface. It is this strange, unconscious instinct that makes it so interesting to biophysicists.
P. polycephalum has demonstrated the ability to ‘model’ and predict environmental stimuli (to which it has mainly responded by increasing or decreasing the speed at which it extended streamers) in previous studies. Scientists have also reported that the number and distribution patterns of its veins can be expressed as regular graphs.
Therefore, a group of Japanese researchers decided to apply the plasmodium to the TSP. They did this by constructing a ‘stellate’ (or star-shaped) resin chip, in which a central circular space was surrounded by 64 lanes of equal width leading to the edge of the chip. This chip was placed on an agar plate nourishing a plasmodium so that the organism was contained within the central circle.
These lanes represented an intercity plan, i.e., one in which n=8, each of which had eight routes leading towards them. The TSP was modeled in this way by observing the manner in which the plasmodium allowed streamers to flow into the channels.
This behavior was optimized by varying the conditions in each channel. For example, if the plasmodium streamed a significant amount of the way along the channel, C3, then all other channels with the designation ‘Cx’ or ‘x3’ were shut off by shining light into them. As this is an undesirable stimulus, the plasmodium would be obliged to find the next best route without ‘visiting’ the same ‘city’ twice.
Therefore, the scientists were able to generate TSP models in which feasible routes were calculated, under conditions such as those above and those in which route length was weighted through illuminating channels (e.g., if the distance between B and C was 50, and that between B and D was 100, the channels representing routes between either city could be illuminated to project how the amoeba would handle this dimension of the problem).
The amoeba was found to be capable of generating these solutions in parallel, whereas those generated by CPUs are done so serially.
The video abstract for the ‘TSP-Solving Amoeba’ paper. (Source: Zhu, L. et al, 2018/ YouTube)
In other words, the method by which the amoeba solved the n=8 TSP would take a conventional processor an unacceptable amount of time to do the same.
On the other hand, CPUs using models and deep learning optimized for their platforms were still able to solve the problem quicker compared to the amoeba. However, the amoeba’s model also allowed for solution numbers with increasing n that is linear rather than exponential, and that can be arrived at in linear time.
This could suggest that, while this bio-processing is still not a match for conventional computing, it may be an option in situations that call for analog, linear-time processing.
This is a promising discovery, especially as next-generation computing may integrate electronics that are inspired by, or even integrate, organisms such as this amoeba and the kind of law-based, parallel processing they perform as part of their nature. Therefore, the future of this discipline may be at least partially biological.
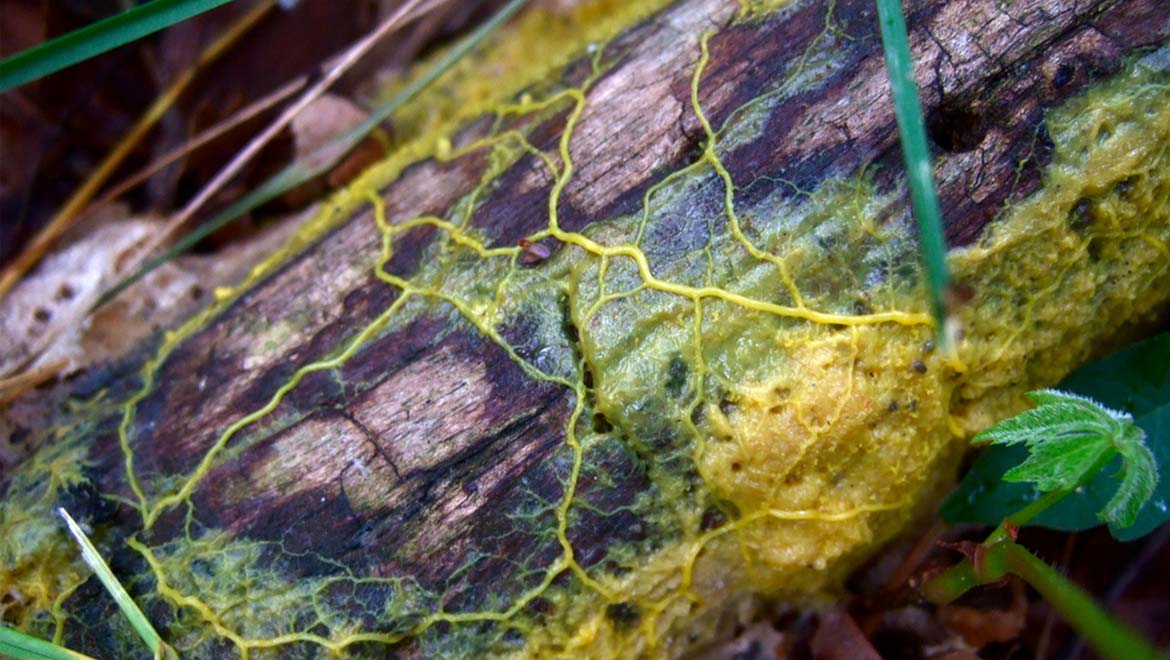
Top Image: A Physarum polycephalum plasmodium sends out streamers along its tree. (Source: Frankenstoen/Flickr)
References
Amoeba finds approximate solutions to NP-hard problem in linear time, 2018, Phys.org, https://phys.org/news/2018-12-amoeba-approximate-solutions-np-hard-problem.html, (accessed 23 Dec. 18)
L. Zhu, et al. Remarkable problem-solving ability of unicellular amoeboid organism and its mechanism. Royal Society Open Science. 5:(12). pp.180396.
W. Baumgarten, et al. (2010) Plasmodial vein networks of the slime mold Physarum polycephalum form regular graphs. Physical Review E. 82:(4). pp.046113.
T. Saigusa, et al. (2008) Amoebae Anticipate Periodic Events. Physical Review Letters. 100:(1). pp.018101.






No comment